Menu principal bas de page

4) Le segment :
Si l'on visualise bien l'image numérique comme un grille de pixels, on comprend que relier deux pixels par un segment revient à trouver sur cette grille le chemin qui s'en rapproche le plus. Pour obtenir le segment on allumera (donnera la couleur du segment) les pixels qui appartiennent à ce chemin.
Le fait que le segment tracé ne paraisse pas droit est appelé "Aliasage".

Ex.: on veut tracer la diagonale d'une image de 9 pixels par 5

On allume les deux pixels extrémités de la diagonale La ligne rouge représente le diagonale mathématique On allume les pixels les plus proches de la ligne rouge

Pour déterminer les pixels à allumer entre les deux pixels extrémités du segment, on dispose de nombreux algorithmes, plus ou moins performants (on mesure la perfomance au temps nécessaire à l’affichage de tout le segment). Tous les algorithmes basés sur la multiplication et la division, gourmands en temps de calcul, on donc été mis de côté. Par contre on peut utiliser des méthodes incrémentales tels que l'algorithme de Bresenham car elles utilisent beaucoup plus d'addition et de soustractions qui sont plus rapides.

a)L'algorithme de Bresenham :
Soit le segment [A, B] au sens mathématique du terme. Les points A et B appartiennent respectivement à 2 pixels M1(x1,y1) et M2(x2,y2). Le problème consiste à déterminer quels pixels on doit allumer pour simuler le tracé d’un segment.

Principe de base :

Il s’agit de diviser l’écran en 8 portions, définis selon les horizontales, les verticales et les diagonales, lesquelles se coupent toutes au centre du pixel M1; Elles définissent ainsi un repère et dessinent 16 régions (on distingue les demi_droites et les portions de plan). M2 se trouve donc dans une de ces 16 régions annotées sur le schéma suivant :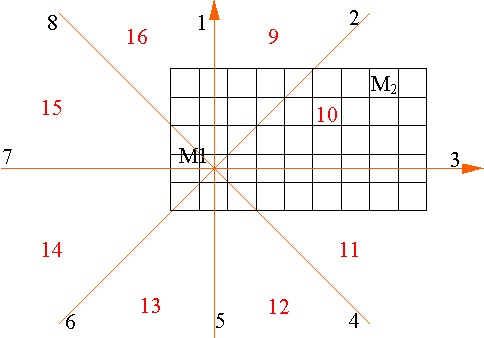


Elimination des cas triviaux :

Si M2 se situe dans les zones numérotées de 1 à 8, c’est à dire sur une des demi-droites tracées, le tracé du segment est extrèmement simple. 2 cas sont alors envisageables : M2 se trouve sur une horizontale ou une vertivale ou M2 appartient à une diagonale. Dans le premier cas, il suffira d’allumer les pixels successivement en se dirigeant en ligne droite vers M2. Dans le deuxième, il suffira d’allumer un pixel horizontalement, puis d’allumer son voisin de dessus (ou dessous selon si M2 est au-dessus, ou au-dessous de M1) et de répéter l’opération jusqu’à arriver en M2.

Autres cas :

Considérons, par exemple, que M2 appartienne à l’octant n°10. Pour tout pixel A(x,y) allumé, les 2 pixels suivants potentiels sont B(x+1,y) et C(x+1,y+1). Quel est le critère de sélèction ?

Remarque : Les coordonnées indiquées sont celles des centres des pixels en question. Toutes sont exprimées dans le nouveau repère centré en M1. De même, en ce qui concerne le dessin suivant, le carré ne représente pas un pixel, mais relie simplement les centres des différents pixels en jeu.



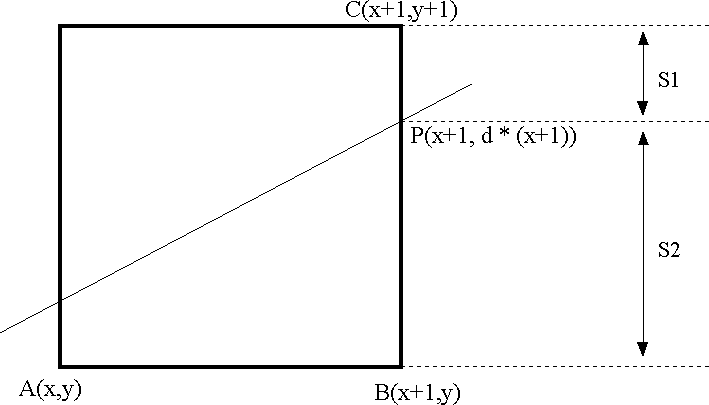
Soit la pente de la droite. Ici, comme M1 est le centre du repère, x1 = 0 = y1.
D’où

Le choix entre B et C s’effectue en fonction de la position du point P(x+1, d * (x +1)) par rapport au centre du segment [BC], c’est à dire en fonction du signe de :

S(a) = S1 - S2
= * S1 - 1
= 2 * (Yp - y) -1
= 2* Yp - 2 * y - 1
= 2 * d * (x+1) - 2 * y -1

Si S(a) > 0, alors S1 > S2. On allume donc le pixel B.
Si S(a) < 0, alors S2 > S1. On allume le pixel C.

Simplification de la méthode de calcul :

Cette méthode paraît extrémement simple à programmer. Cependant, elle couterait cher en temps de calcul si on utilisait la formule tel quelle, du fait des diverses multiplications à réaliser. Il serait préférable d'utiliser une récurrence, ce qui permettrait de calculer directement " le S " d’un pixel à partir celui de son prédécesseur en une simple opération.

Remarquons ceci :
Si S(a) > 0, on allume B et S(b) = 2 * d * (x + 2) - 2 * y - 1 (on remplace dans la formule x par x+1)
= 2 * d * x + 4 * d - 2 * y - 1
= S(a) + 2 * d


Le pixel B a été allumé. On cherche S(b)


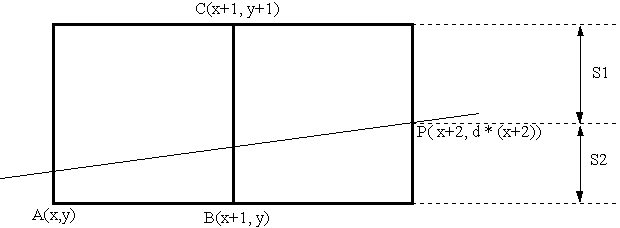
Si S(a) < 0, on allume C et S(c) = 2 * d * (x + 2) - 2 * (y + 1) - 1
= 2 * d * x + 4 * d - 2 * y - 2 - 1
= S(a) + 2 * d - 2

Le pixel C a été allumé. On cherche S(c)


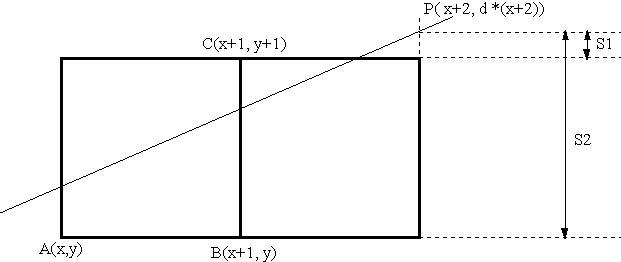
Ainsi, selon le signe de S(a), on peut calculer par une simple addition, "le S " du pixel suivant. Il manque cependant à la récurrence son 1er élément : le pixel de coordonnées (0,0) pour lequel S(M1) = 2 * d - 1. La récurrence est donc complète, l’algorithme la concrétisant est alors facile à élaborer. Le voici en pseudo-langage : 

Début
  d = y2 / x2
  S = 2 * d - 1
  Inc1 = 2 * d
  Inc2 = 2* d - 2
  Y = 0
  Pour x allant de 0 à x2 incrément 1
     Faire
        Afficher (x,y) 
        Si S < 0 alors S = S + Inc1
                       Sinon 
		 Faire
		    S = S + Inc2
		    y = y+1
		FinFaire
     FinFaire	
Fin
b) Remarque :
On travaille souvent sur des objets linéaires (droites, segments) Cela présente l'avantage suivant : il suffit pour calculer l'image d'un objet, de calculer les images de quelques points caractéristiques au lieu de le faire pour tous les points, ensuite, il ne reste plus qu’à relier ces points images.

Par exemple, pour tracer un rectangle, il suffira de donner les quatre sommets puis de tracer les segment entre ceux-ci. Si on lui fait subir une rotation, on appliquera la rotation aux quatre sommets puis on recommencera le tracé des côtés.

5)Les figures simples :

Beaucoup d’application utilise d’autres primitives graphiques qui sont des formes simples, comme des rectangles ou des cercles. Il est courant aujourd’hui que la génération de tels primitives soit câblée (réalisée par un matériel spécifique), il suffit dans ce cas d’envoyer juste un code précis pour obtenir ce que l’on veut (pour un cercle ce sera les coordonnées du centre et le rayon). Mais si ce n’est pas le cas, il faut générer par programme. Nous ne le ferons pas car le langage que nous avons décidé d’utilisé (Pascal) est simple mais inadapté.


Page
précédente 		Page
suivante