III/ Le passage de la 3D à la 2D :
III/ Le passage de la 3D à la 2D :
 L’écran étant une surface plane, toute image de plus de deux dimensions devra être modifiée pour pourvoir y être représentée. Ainsi, il est nécessaire de réaliser ce que l’on appelle les projections. Ce sont des outils permettant d’enlever une dimension, passer de la 3D à la 2D. La catégorie de projections qui nous intéresse est celle qui est connue sous le nom de projections planes, par oppositions à celle des projections sur surface courbe.
L’écran étant une surface plane, toute image de plus de deux dimensions devra être modifiée pour pourvoir y être représentée. Ainsi, il est nécessaire de réaliser ce que l’on appelle les projections. Ce sont des outils permettant d’enlever une dimension, passer de la 3D à la 2D. La catégorie de projections qui nous intéresse est celle qui est connue sous le nom de projections planes, par oppositions à celle des projections sur surface courbe.
 Il existe deux grands types de projections planes : les projections parallèles et les projections perspectives. Chacune possède ses avantages et ses inconvénients. Les " parallèles " sont simples à mettre en oeuvre mais elles ne sont pas très réalistes contrairement aux projections perspectives. Celles-ci donnent mieux l’illusion d‘une image 3D.
Il existe deux grands types de projections planes : les projections parallèles et les projections perspectives. Chacune possède ses avantages et ses inconvénients. Les " parallèles " sont simples à mettre en oeuvre mais elles ne sont pas très réalistes contrairement aux projections perspectives. Celles-ci donnent mieux l’illusion d‘une image 3D.

 1) Les projections parallèles :
1) Les projections parallèles :
Il en existe deux grandes variantes, qui possèdent toutes des caractères communs :
 - le centre de projection (point de fuite) se trouve à l'infinie, les rayons de projections sont donc parallèles
- le centre de projection (point de fuite) se trouve à l'infinie, les rayons de projections sont donc parallèles
 - le parallélisme est conservé
- le parallélisme est conservé
 - les angles et les distances inclues dans une face parallèle au plan de projection restent invariables.
- les angles et les distances inclues dans une face parallèle au plan de projection restent invariables.
On les met en œuvre en projetant chaque point selon une droite de référence sur le plan de projection. Cette droite passera par un point de l'objet et son image sur le plan.
Elles sont souvent utilisées car elles permettent de mesurer les dimensions de l’objet (pas de déformations) et sont simples à dessiner.

 a) Projection axonométrique :
a) Projection axonométrique :
 Les projections axonométriques permettent de choisir librement un angle d’observation, c’est à dire, l’angle formé par la droite de projection et le plan du même nom.
Les projections axonométriques permettent de choisir librement un angle d’observation, c’est à dire, l’angle formé par la droite de projection et le plan du même nom.
Elles possèdent quelques propriétés qu’il est important de noter :
 - Le parallélisme est conservé, les angles sont en général modifiés.
- Le parallélisme est conservé, les angles sont en général modifiés.
 - Le raccourcissement des distances est uniforme : toute modification intervenant sur l'objet à projeter sera reproduite de la même façon sur son image.
- Le raccourcissement des distances est uniforme : toute modification intervenant sur l'objet à projeter sera reproduite de la même façon sur son image.
 - Le fait de rapprocher l’objet du plan de projection ne modifiera en aucun cas la taille de sa représentation.
- Le fait de rapprocher l’objet du plan de projection ne modifiera en aucun cas la taille de sa représentation.

 On distingue trois types de projections axonométriques : l’orthogonale, la dimétrique et l’isométrique.
On distingue trois types de projections axonométriques : l’orthogonale, la dimétrique et l’isométrique.
 Pour la première, l'angle d'observation est égal à 90 degrés. La direction de projection est donc orthogonale au plan de projection, lui-même parallèle à l'un des axes principaux. Elle est très utilisée en dessin technique, dans le cas où 2 vecteurs unitaires (
Pour la première, l'angle d'observation est égal à 90 degrés. La direction de projection est donc orthogonale au plan de projection, lui-même parallèle à l'un des axes principaux. Elle est très utilisée en dessin technique, dans le cas où 2 vecteurs unitaires ( ,
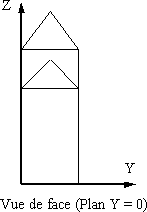
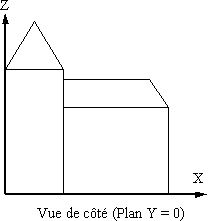
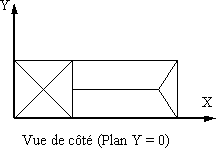
,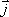 ) se trouvent dans le plan de projection, pour obtenir les vues de face, de dessus et de côté. Dans ce cas, projeter revient à éliminer la coordonnée définie par le vecteur
) se trouvent dans le plan de projection, pour obtenir les vues de face, de dessus et de côté. Dans ce cas, projeter revient à éliminer la coordonnée définie par le vecteur 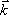 .
.
Pour les deux autres, le plan de projection n'est parallèle à aucun des 3 plans définis par les axes du repère. Cependant,
 Si deux des vecteurs unitaires sont, après projection, de même longueur, il s'agira d'une projection dimétrique. On constatera alors un changement d'échelle pour l'une des trois projections des vecteurs unitaires. C'est donc une projection déformatrice.
Si deux des vecteurs unitaires sont, après projection, de même longueur, il s'agira d'une projection dimétrique. On constatera alors un changement d'échelle pour l'une des trois projections des vecteurs unitaires. C'est donc une projection déformatrice.
 Si tous les vecteurs unitaires sont, après projection, de même longueur, ce sera une projection isométrique. Elle est fréquemment utilisée en dessin manuel car, à partir des coordonnées des points, il est très facile de tracer le dessin (pas besoin de recalculer les distances selon chaque axe).
Si tous les vecteurs unitaires sont, après projection, de même longueur, ce sera une projection isométrique. Elle est fréquemment utilisée en dessin manuel car, à partir des coordonnées des points, il est très facile de tracer le dessin (pas besoin de recalculer les distances selon chaque axe).
 b) Les projections obliques :
b) Les projections obliques :
 Voici la caractéristique principale de ce type de projection : le plan de projection est perpendiculaire, non plus à la direction de projection comme précédemment, mais à l’un des axes du repère de l’objet.
Voici la caractéristique principale de ce type de projection : le plan de projection est perpendiculaire, non plus à la direction de projection comme précédemment, mais à l’un des axes du repère de l’objet.
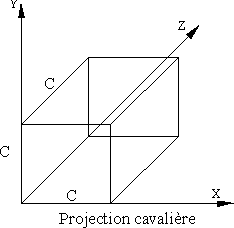
Les deux projections obliques les plus connues sont la projection cavalière et la projection cabinet.
Pour la première, la direction de projection fait un angle de 45° avec le plan de projection et les distances ne sont pas réduites. Les lignes fuyantes sont dessinées généralement avec un angle de 30 ou 45° avec l’horizontale.
Définition : les lignes fuyantes sont les arrêtes qui, prolongées à l’infinie, s’en vont vers le centre de projection (point de fuite)
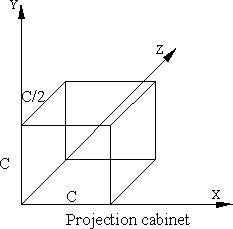
 Dans la seconde, on raccourcit les arrêtes portées par les lignes fuyantes dans le rapport de ½. De ce fait, la projection cabinet et plus réaliste que la projection cavalière.
Dans la seconde, on raccourcit les arrêtes portées par les lignes fuyantes dans le rapport de ½. De ce fait, la projection cabinet et plus réaliste que la projection cavalière.

 III/ Le passage de la 3D à la 2D :
III/ Le passage de la 3D à la 2D : L’écran étant une surface plane, toute image de plus de deux dimensions devra être modifiée pour pourvoir y être représentée. Ainsi, il est nécessaire de réaliser ce que l’on appelle les projections. Ce sont des outils permettant d’enlever une dimension, passer de la 3D à la 2D. La catégorie de projections qui nous intéresse est celle qui est connue sous le nom de projections planes, par oppositions à celle des projections sur surface courbe.
L’écran étant une surface plane, toute image de plus de deux dimensions devra être modifiée pour pourvoir y être représentée. Ainsi, il est nécessaire de réaliser ce que l’on appelle les projections. Ce sont des outils permettant d’enlever une dimension, passer de la 3D à la 2D. La catégorie de projections qui nous intéresse est celle qui est connue sous le nom de projections planes, par oppositions à celle des projections sur surface courbe. Il existe deux grands types de projections planes : les projections parallèles et les projections perspectives. Chacune possède ses avantages et ses inconvénients. Les " parallèles " sont simples à mettre en oeuvre mais elles ne sont pas très réalistes contrairement aux projections perspectives. Celles-ci donnent mieux l’illusion d‘une image 3D.
Il existe deux grands types de projections planes : les projections parallèles et les projections perspectives. Chacune possède ses avantages et ses inconvénients. Les " parallèles " sont simples à mettre en oeuvre mais elles ne sont pas très réalistes contrairement aux projections perspectives. Celles-ci donnent mieux l’illusion d‘une image 3D.
 1) Les projections parallèles :
1) Les projections parallèles :  - le centre de projection (point de fuite) se trouve à l'infinie, les rayons de projections sont donc parallèles
- le centre de projection (point de fuite) se trouve à l'infinie, les rayons de projections sont donc parallèles  - le parallélisme est conservé
- le parallélisme est conservé  - les angles et les distances inclues dans une face parallèle au plan de projection restent invariables.
- les angles et les distances inclues dans une face parallèle au plan de projection restent invariables.
 a) Projection axonométrique :
a) Projection axonométrique : Les projections axonométriques permettent de choisir librement un angle d’observation, c’est à dire, l’angle formé par la droite de projection et le plan du même nom.
Les projections axonométriques permettent de choisir librement un angle d’observation, c’est à dire, l’angle formé par la droite de projection et le plan du même nom.  - Le parallélisme est conservé, les angles sont en général modifiés.
- Le parallélisme est conservé, les angles sont en général modifiés. - Le raccourcissement des distances est uniforme : toute modification intervenant sur l'objet à projeter sera reproduite de la même façon sur son image.
- Le raccourcissement des distances est uniforme : toute modification intervenant sur l'objet à projeter sera reproduite de la même façon sur son image. - Le fait de rapprocher l’objet du plan de projection ne modifiera en aucun cas la taille de sa représentation.
- Le fait de rapprocher l’objet du plan de projection ne modifiera en aucun cas la taille de sa représentation.
 On distingue trois types de projections axonométriques : l’orthogonale, la dimétrique et l’isométrique.
On distingue trois types de projections axonométriques : l’orthogonale, la dimétrique et l’isométrique. Pour la première, l'angle d'observation est égal à 90 degrés. La direction de projection est donc orthogonale au plan de projection, lui-même parallèle à l'un des axes principaux. Elle est très utilisée en dessin technique, dans le cas où 2 vecteurs unitaires (
Pour la première, l'angle d'observation est égal à 90 degrés. La direction de projection est donc orthogonale au plan de projection, lui-même parallèle à l'un des axes principaux. Elle est très utilisée en dessin technique, dans le cas où 2 vecteurs unitaires ( ,
,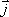 ) se trouvent dans le plan de projection, pour obtenir les vues de face, de dessus et de côté. Dans ce cas, projeter revient à éliminer la coordonnée définie par le vecteur
) se trouvent dans le plan de projection, pour obtenir les vues de face, de dessus et de côté. Dans ce cas, projeter revient à éliminer la coordonnée définie par le vecteur 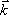 .
.
 Si deux des vecteurs unitaires sont, après projection, de même longueur, il s'agira d'une projection dimétrique. On constatera alors un changement d'échelle pour l'une des trois projections des vecteurs unitaires. C'est donc une projection déformatrice.
Si deux des vecteurs unitaires sont, après projection, de même longueur, il s'agira d'une projection dimétrique. On constatera alors un changement d'échelle pour l'une des trois projections des vecteurs unitaires. C'est donc une projection déformatrice. Si tous les vecteurs unitaires sont, après projection, de même longueur, ce sera une projection isométrique. Elle est fréquemment utilisée en dessin manuel car, à partir des coordonnées des points, il est très facile de tracer le dessin (pas besoin de recalculer les distances selon chaque axe).
Si tous les vecteurs unitaires sont, après projection, de même longueur, ce sera une projection isométrique. Elle est fréquemment utilisée en dessin manuel car, à partir des coordonnées des points, il est très facile de tracer le dessin (pas besoin de recalculer les distances selon chaque axe). b) Les projections obliques :
b) Les projections obliques : Voici la caractéristique principale de ce type de projection : le plan de projection est perpendiculaire, non plus à la direction de projection comme précédemment, mais à l’un des axes du repère de l’objet.
Voici la caractéristique principale de ce type de projection : le plan de projection est perpendiculaire, non plus à la direction de projection comme précédemment, mais à l’un des axes du repère de l’objet. Dans la seconde, on raccourcit les arrêtes portées par les lignes fuyantes dans le rapport de ½. De ce fait, la projection cabinet et plus réaliste que la projection cavalière.
Dans la seconde, on raccourcit les arrêtes portées par les lignes fuyantes dans le rapport de ½. De ce fait, la projection cabinet et plus réaliste que la projection cavalière.