
 Jusqu'ici, nous avons étudié diverses méthodes mathématiques permettant la visualisation des objets en 3D sur un écran en 2D. Cependant, il est nécessaire de chercher à réduire au maximum les calculs, car ils sont déjà nombreux pour des figures simples, et d'améliorer le rendu final de l'objet.
Jusqu'ici, nous avons étudié diverses méthodes mathématiques permettant la visualisation des objets en 3D sur un écran en 2D. Cependant, il est nécessaire de chercher à réduire au maximum les calculs, car ils sont déjà nombreux pour des figures simples, et d'améliorer le rendu final de l'objet.
 C'est à cela que servent les algorithmes complémentaires suivants : le découpage de Cohen et Sutherland, les plans frontaux et l'algorithme d'élimination des faces cachées.
C'est à cela que servent les algorithmes complémentaires suivants : le découpage de Cohen et Sutherland, les plans frontaux et l'algorithme d'élimination des faces cachées.
 I/ Découpage de Cohen et Sutherland :
I/ Découpage de Cohen et Sutherland :
 1) Principe du découpage :
1) Principe du découpage :
 L’algorithme de découpage de Cohen et Sutherland permet de réduire la quantité de calcul nécessaire à la restitution de l’espace 3D sur l’écran et d’éviter quelques erreurs, généralement fatale, causée par une tentative de tracé d’un segment sortant des limites de l’écran, ceci en déterminant quelle portion de l’espace sera projeté sur l’écran.
L’algorithme de découpage de Cohen et Sutherland permet de réduire la quantité de calcul nécessaire à la restitution de l’espace 3D sur l’écran et d’éviter quelques erreurs, généralement fatale, causée par une tentative de tracé d’un segment sortant des limites de l’écran, ceci en déterminant quelle portion de l’espace sera projeté sur l’écran.
 En effet, si on regarde devant soi, on ne perçoit qu’une fraction de l’espace qui nous entoure. Ce que l’on voit appartient à un cône, centré sur l’axe Z ayant pour sommet l’œil. Cependant, l’écran étant rectangulaire et non infini comme le plan de projection (cf. projection en perspective), nous avons choisi de remplacer ce cône par une pyramide.
En effet, si on regarde devant soi, on ne perçoit qu’une fraction de l’espace qui nous entoure. Ce que l’on voit appartient à un cône, centré sur l’axe Z ayant pour sommet l’œil. Cependant, l’écran étant rectangulaire et non infini comme le plan de projection (cf. projection en perspective), nous avons choisi de remplacer ce cône par une pyramide.

 Etant donné que nous avons décidé dans notre programme de considérer le segment comme unité graphique, nous allons résonner sur ce dernier.
Etant donné que nous avons décidé dans notre programme de considérer le segment comme unité graphique, nous allons résonner sur ce dernier.
Considérons le segment [AB]. Trois cas peuvent se produire :
 - [AB] se situe entièrement dans la pyramide.
- [AB] se situe entièrement dans la pyramide.
 - [AB] se situe entièrement hors de la pyramide.
- [AB] se situe entièrement hors de la pyramide.
 - [AB] coupe la pyramide en un (1 des points se situe à l’extérieur, l’autre à l’intérieur) ou deux points (A et B se trouvent hors de la pyramide).
- [AB] coupe la pyramide en un (1 des points se situe à l’extérieur, l’autre à l’intérieur) ou deux points (A et B se trouvent hors de la pyramide).
Dans le premier cas, le segment est totalement dans la pyramide. Il doit donc être entièrement projeté sur la surface de l’écran.
Le second cas est totalement inverse : le segment ne se trouve pas dans la pyramide. Il ne faut donc pas l’afficher. On ne réalisera donc pas les calculs le concernant.
Enfin, le troisième cas est beaucoup plus complexe. Il est nécessaire de le détailler puisque l’on distingue plusieurs sous-cas.
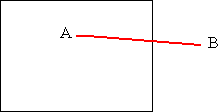
 - 1er cas : A en dehors de la pyramide, B dedans.
- 1er cas : A en dehors de la pyramide, B dedans.
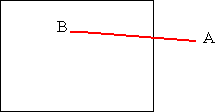
 - 2ème cas : B en dehors de la pyramide, A dedans (analogue au précédent).
- 2ème cas : B en dehors de la pyramide, A dedans (analogue au précédent).
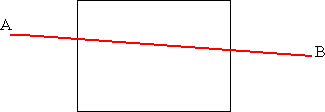
 - 3ème cas : A et B sont en dehors de la pyramide, mais [AB] coupe celle-ci.
- 3ème cas : A et B sont en dehors de la pyramide, mais [AB] coupe celle-ci.
Note : Pour représenter le segment et l’écran nous adopterons une vue de face en se plaçant du côté de l’œil, en projetant orthogonalement.
 | | 1er cas |
|
 | | 2ème cas |
|
 | | 3ème cas |
|
Le problème revient à calculer les coordonnées du point d’intersection entre le segment [AB] et un des plan de la pyramide.
 2) Algorithme du découpage :
2) Algorithme du découpage :
La procédure algorithmique se réalise en 3 étapes :
 - On teste la position de chaque extrémité du segment.
- On teste la position de chaque extrémité du segment.
 - On code les résultats en binaire sur un octet.
- On code les résultats en binaire sur un octet.
 - On réalise les différents calculs de découpage.
- On réalise les différents calculs de découpage.
 a) Test de visiblité :
a) Test de visiblité :
Observons la pyramide de profil :
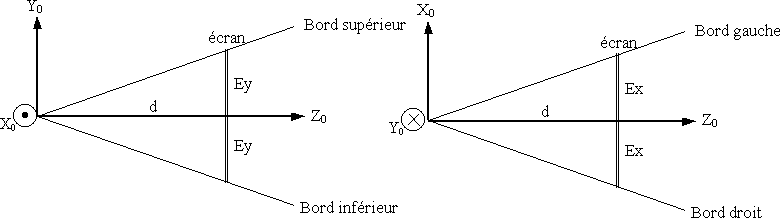
Ex : demi-longueur de l’écran selon l’axe X.
Ey : demi-longueur de l’écran selon l’axe Y.
Pour être visible, un point doit appartenir à la pyramide. Si on considère un point quelconque de l’espace P(x,y,z), les conditions de visibilité sont les suivantes :
 - y < Ey * z / d car P doit être en-dessous du plan supérieur.
- y < Ey * z / d car P doit être en-dessous du plan supérieur.
 - y > -Ey * z / d car P doit être au-dessus du plan inférieur.
- y > -Ey * z / d car P doit être au-dessus du plan inférieur.
 - x < Ex * z / d car P doit être à gauche du plan droit.
- x < Ex * z / d car P doit être à gauche du plan droit.
 - x > -Ex * z / d car P doit être à droite du plan gauche.
- x > -Ex * z / d car P doit être à droite du plan gauche.
Ces formules sont obtenues en prenant les formules de projection en perspective (vues précédemment) et en les appliquant avec les demi-longueurs de l’écran (on prend X = Ex, Y = Ey).
 b) Codage des résultats :
b) Codage des résultats :
 Principe :
Principe :
 Pour des raisons de rapidité et de simplicité, il convient non pas d’utiliser 4 variables booléennes, une pour chaque position possible (au-dessus, en-dessous, à droite et à gauche de la pyramide), mais de coder cela en prenant 1 bit à la place de chacune de ces variables. Cela sera possible en affectant à chaque point une variable " position " d’un octet indiquant sa position.
Pour des raisons de rapidité et de simplicité, il convient non pas d’utiliser 4 variables booléennes, une pour chaque position possible (au-dessus, en-dessous, à droite et à gauche de la pyramide), mais de coder cela en prenant 1 bit à la place de chacune de ces variables. Cela sera possible en affectant à chaque point une variable " position " d’un octet indiquant sa position.
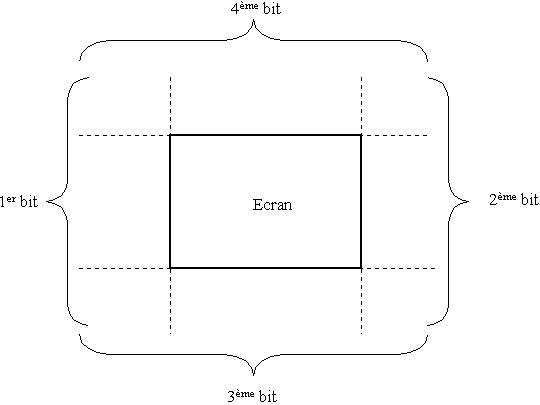
Si le point se trouve à droite du bord gauche de la pyramide, on allume le 1er bit de la variable "position", à gauche du bord droit de la pyramide, le 2ème bit, en-dessous du bord inférieur, le 3ème bit, et au-dessus du bord supérieur, le 4ème bit.
Exemple : Si le point se trouve à gauche et au-dessus de la pyramide, sa variable position aura les bits n°1 et 4 allumés.
 Table de correspondance :
Table de correspondance :
 Sachant que l’on travaille sur les bits d’un octet, ce dernier va contenir une valeur entière indiquant la position du point auquel la variable est affectée. Voici le tableau de correspondance, utilisé dans notre programme :
Sachant que l’on travaille sur les bits d’un octet, ce dernier va contenir une valeur entière indiquant la position du point auquel la variable est affectée. Voici le tableau de correspondance, utilisé dans notre programme :
| Position du point |
Valeur de la variable position |
Position du point |
Valeur de la variable position |
| milieu |
0 (00000000) |
Bas gauche |
5 (00000101) |
| Gauche |
1 (00000001) |
Bas droite |
6 (00000110) |
| Droite |
2 (00000010) |
Haut gauche |
9 (00001001) |
| Bas |
4 (00000100) |
Haut droite |
10 (00001010) |
| Haut |
8 (00001000) |
|
|
 Avantages du codage :
Avantages du codage :
 - Le nombre de test nécessaire pour déterminer la position du point est plus petit que si on avait utiliser 4 variables différentes.
- Le nombre de test nécessaire pour déterminer la position du point est plus petit que si on avait utiliser 4 variables différentes.
 - Si la variable position est nulle, le point se trouve à l’intérieur de l’écran.
- Si la variable position est nulle, le point se trouve à l’intérieur de l’écran.
 - Pour savoir si le segment [AB] appartient entièrement à la pyramide, il suffit que le " ET " logique des variables positions de A et B soit non nul.
- Pour savoir si le segment [AB] appartient entièrement à la pyramide, il suffit que le " ET " logique des variables positions de A et B soit non nul.
Ex : A en haut à gauche, B en haut. Position(A) = 9, Position(B)= 8.
| (00001000) |
and |
(00001001) |
= |
(00000001) |
| 8 |
and |
9 |
= |
1 |
 Le traduire en Pascal ?
Le traduire en Pascal ?
 - Pour allumer le 3-ième bit de la variable " position " (1 octet) , il suffit d’utiliser l’instruction suivante :
- Pour allumer le 3-ième bit de la variable " position " (1 octet) , il suffit d’utiliser l’instruction suivante :
position = position or (00000100)
Ce qui équivaut à : position = position or 4
 - Pour tester si le 7-ième bit de la variable " position ", il suffit d’utiliser l’instruction de test suivante :
- Pour tester si le 7-ième bit de la variable " position ", il suffit d’utiliser l’instruction de test suivante :
If (position and (01000000) = (01000000) then ...
Ce qui équivaut à : If (position and 64) = 64 then ...
 c) Le découpage :
c) Le découpage :
 Maintenant, que les différents cas ont été établis, que l’on sait où se trouve le point litigieux, et que l’on a mis à jour sa variable position, on peut procéder au découpage proprement-dit. Il s’agit de calculer les coordonnées du point d’intersection entre le segment et le ou les bords concernés de la pyramide.
Maintenant, que les différents cas ont été établis, que l’on sait où se trouve le point litigieux, et que l’on a mis à jour sa variable position, on peut procéder au découpage proprement-dit. Il s’agit de calculer les coordonnées du point d’intersection entre le segment et le ou les bords concernés de la pyramide.
L’équation d’une droite de l’espace comprenant deux points (x1,y1,z1) et (x2,y2,z2) est :
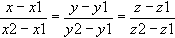
| Sous forme paramétrique, cela donne : |
 |
Cherchons l’intersection de cette droite avec le plan supérieur par exemple. Il faut résoudre le système suivant :

| On en déduit par substitution, sur Y et Z : |
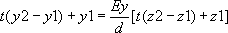 |
| Et finalement : |
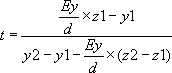 |
Si l’on remplace t par sa valeur dans le système d’équations paramétriques, on obtient les coordonnées (x,y,z) du point d’intersection cherché.
Par un calcul similaire, on obtient t pour les autres plans :
 - intersection avec le plan inférieur (bit n°3 allumé) : - intersection avec le plan inférieur (bit n°3 allumé) : |
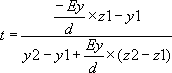 |
 - intersection avec le plan de gauche (bit n°1 allumé) : - intersection avec le plan de gauche (bit n°1 allumé) : |
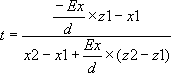 |
 - intersection avec le plan de droite (bit n° 2 allumé) : - intersection avec le plan de droite (bit n° 2 allumé) : |
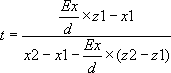 |
 d) Cas particuliers :
d) Cas particuliers :
 Dans certains cas, la procédure de découpage est plus longue.
Dans certains cas, la procédure de découpage est plus longue.
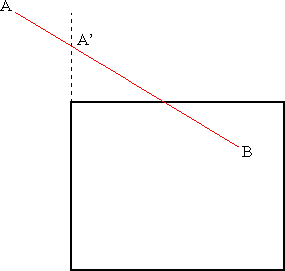
 En effet, si par exemple A est au-dessus à gauche de la pyramide, B dans la pyramide de vision, il sera nécessaire de calculer l'intersection avec le plan supérieur et le plan gauche. Détaillons la marche à suivre :
En effet, si par exemple A est au-dessus à gauche de la pyramide, B dans la pyramide de vision, il sera nécessaire de calculer l'intersection avec le plan supérieur et le plan gauche. Détaillons la marche à suivre :
|
 |
On calcule l'intersection entre [AB] et le plan gauche. On obtient le point A' se trouvant sur le plan gauche, mais ne faisant pas forcément partie de la pyramide. A' remplace A car [AA'] est forcément à l'extérieur de la pyramide. |
 |
| Cas complexe : A' n'appartient pas à la pyramide |
|
 |
Pour savoir où se trouve A’, on calcule la variable "position" de A’. Deux cas sont possibles : Soit la variable est nulle (A’ appartient à la pyramide), soit elle ne l’est pas. Il faut alors calculer l’intersection entre [A’B] et le plan supérieur, qui est le seul restant en jeu. On obtient le point A’’, qui appartient de manière certaine à la pyramide. |
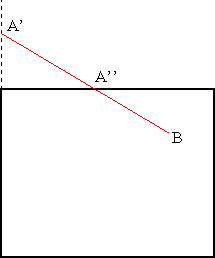 |
| Fin du processus : A'' appartient à la pyramide |
|
 |
Si A et B sont extérieurs à la pyramide, mais que [AB] la coupe, alors il faut réaliser un double découpage, un concernant A, l’autre concernant B. |


 Jusqu'ici, nous avons étudié diverses méthodes mathématiques permettant la visualisation des objets en 3D sur un écran en 2D. Cependant, il est nécessaire de chercher à réduire au maximum les calculs, car ils sont déjà nombreux pour des figures simples, et d'améliorer le rendu final de l'objet.
Jusqu'ici, nous avons étudié diverses méthodes mathématiques permettant la visualisation des objets en 3D sur un écran en 2D. Cependant, il est nécessaire de chercher à réduire au maximum les calculs, car ils sont déjà nombreux pour des figures simples, et d'améliorer le rendu final de l'objet.  C'est à cela que servent les algorithmes complémentaires suivants : le découpage de Cohen et Sutherland, les plans frontaux et l'algorithme d'élimination des faces cachées.
C'est à cela que servent les algorithmes complémentaires suivants : le découpage de Cohen et Sutherland, les plans frontaux et l'algorithme d'élimination des faces cachées. I/ Découpage de Cohen et Sutherland :
I/ Découpage de Cohen et Sutherland :  1) Principe du découpage :
1) Principe du découpage : L’algorithme de découpage de Cohen et Sutherland permet de réduire la quantité de calcul nécessaire à la restitution de l’espace 3D sur l’écran et d’éviter quelques erreurs, généralement fatale, causée par une tentative de tracé d’un segment sortant des limites de l’écran, ceci en déterminant quelle portion de l’espace sera projeté sur l’écran.
L’algorithme de découpage de Cohen et Sutherland permet de réduire la quantité de calcul nécessaire à la restitution de l’espace 3D sur l’écran et d’éviter quelques erreurs, généralement fatale, causée par une tentative de tracé d’un segment sortant des limites de l’écran, ceci en déterminant quelle portion de l’espace sera projeté sur l’écran. En effet, si on regarde devant soi, on ne perçoit qu’une fraction de l’espace qui nous entoure. Ce que l’on voit appartient à un cône, centré sur l’axe Z ayant pour sommet l’œil. Cependant, l’écran étant rectangulaire et non infini comme le plan de projection (cf. projection en perspective), nous avons choisi de remplacer ce cône par une pyramide.
En effet, si on regarde devant soi, on ne perçoit qu’une fraction de l’espace qui nous entoure. Ce que l’on voit appartient à un cône, centré sur l’axe Z ayant pour sommet l’œil. Cependant, l’écran étant rectangulaire et non infini comme le plan de projection (cf. projection en perspective), nous avons choisi de remplacer ce cône par une pyramide.
 Etant donné que nous avons décidé dans notre programme de considérer le segment comme unité graphique, nous allons résonner sur ce dernier.
Etant donné que nous avons décidé dans notre programme de considérer le segment comme unité graphique, nous allons résonner sur ce dernier.
 - [AB] se situe entièrement dans la pyramide.
- [AB] se situe entièrement dans la pyramide. - [AB] se situe entièrement hors de la pyramide.
- [AB] se situe entièrement hors de la pyramide. - [AB] coupe la pyramide en un (1 des points se situe à l’extérieur, l’autre à l’intérieur) ou deux points (A et B se trouvent hors de la pyramide).
- [AB] coupe la pyramide en un (1 des points se situe à l’extérieur, l’autre à l’intérieur) ou deux points (A et B se trouvent hors de la pyramide). - 1er cas : A en dehors de la pyramide, B dedans.
- 1er cas : A en dehors de la pyramide, B dedans. - 2ème cas : B en dehors de la pyramide, A dedans (analogue au précédent).
- 2ème cas : B en dehors de la pyramide, A dedans (analogue au précédent). - 3ème cas : A et B sont en dehors de la pyramide, mais [AB] coupe celle-ci.
- 3ème cas : A et B sont en dehors de la pyramide, mais [AB] coupe celle-ci. 2) Algorithme du découpage :
2) Algorithme du découpage : - On teste la position de chaque extrémité du segment.
- On teste la position de chaque extrémité du segment. - On code les résultats en binaire sur un octet.
- On code les résultats en binaire sur un octet. - On réalise les différents calculs de découpage.
- On réalise les différents calculs de découpage. a) Test de visiblité :
a) Test de visiblité :
 - y < Ey * z / d car P doit être en-dessous du plan supérieur.
- y < Ey * z / d car P doit être en-dessous du plan supérieur. - y > -Ey * z / d car P doit être au-dessus du plan inférieur.
- y > -Ey * z / d car P doit être au-dessus du plan inférieur.
 - x < Ex * z / d car P doit être à gauche du plan droit.
- x < Ex * z / d car P doit être à gauche du plan droit. - x > -Ex * z / d car P doit être à droite du plan gauche.
- x > -Ex * z / d car P doit être à droite du plan gauche. b) Codage des résultats :
b) Codage des résultats : Principe :
Principe : Pour des raisons de rapidité et de simplicité, il convient non pas d’utiliser 4 variables booléennes, une pour chaque position possible (au-dessus, en-dessous, à droite et à gauche de la pyramide), mais de coder cela en prenant 1 bit à la place de chacune de ces variables. Cela sera possible en affectant à chaque point une variable " position " d’un octet indiquant sa position.
Pour des raisons de rapidité et de simplicité, il convient non pas d’utiliser 4 variables booléennes, une pour chaque position possible (au-dessus, en-dessous, à droite et à gauche de la pyramide), mais de coder cela en prenant 1 bit à la place de chacune de ces variables. Cela sera possible en affectant à chaque point une variable " position " d’un octet indiquant sa position.
 Table de correspondance :
Table de correspondance :  Sachant que l’on travaille sur les bits d’un octet, ce dernier va contenir une valeur entière indiquant la position du point auquel la variable est affectée. Voici le tableau de correspondance, utilisé dans notre programme :
Sachant que l’on travaille sur les bits d’un octet, ce dernier va contenir une valeur entière indiquant la position du point auquel la variable est affectée. Voici le tableau de correspondance, utilisé dans notre programme : Avantages du codage :
Avantages du codage : - Le nombre de test nécessaire pour déterminer la position du point est plus petit que si on avait utiliser 4 variables différentes.
- Le nombre de test nécessaire pour déterminer la position du point est plus petit que si on avait utiliser 4 variables différentes. - Si la variable position est nulle, le point se trouve à l’intérieur de l’écran.
- Si la variable position est nulle, le point se trouve à l’intérieur de l’écran.  - Pour savoir si le segment [AB] appartient entièrement à la pyramide, il suffit que le " ET " logique des variables positions de A et B soit non nul.
- Pour savoir si le segment [AB] appartient entièrement à la pyramide, il suffit que le " ET " logique des variables positions de A et B soit non nul. Le traduire en Pascal ?
Le traduire en Pascal ? - Pour allumer le 3-ième bit de la variable " position " (1 octet) , il suffit d’utiliser l’instruction suivante :
- Pour allumer le 3-ième bit de la variable " position " (1 octet) , il suffit d’utiliser l’instruction suivante :  - Pour tester si le 7-ième bit de la variable " position ", il suffit d’utiliser l’instruction de test suivante :
- Pour tester si le 7-ième bit de la variable " position ", il suffit d’utiliser l’instruction de test suivante : c) Le découpage :
c) Le découpage :  Maintenant, que les différents cas ont été établis, que l’on sait où se trouve le point litigieux, et que l’on a mis à jour sa variable position, on peut procéder au découpage proprement-dit. Il s’agit de calculer les coordonnées du point d’intersection entre le segment et le ou les bords concernés de la pyramide.
Maintenant, que les différents cas ont été établis, que l’on sait où se trouve le point litigieux, et que l’on a mis à jour sa variable position, on peut procéder au découpage proprement-dit. Il s’agit de calculer les coordonnées du point d’intersection entre le segment et le ou les bords concernés de la pyramide.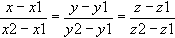


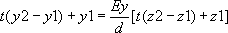
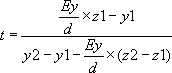
 - intersection avec le plan inférieur (bit n°3 allumé) :
- intersection avec le plan inférieur (bit n°3 allumé) : 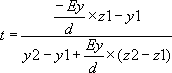
 - intersection avec le plan de gauche (bit n°1 allumé) :
- intersection avec le plan de gauche (bit n°1 allumé) :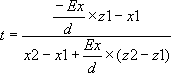
 - intersection avec le plan de droite (bit n° 2 allumé) :
- intersection avec le plan de droite (bit n° 2 allumé) :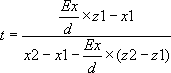
 d) Cas particuliers :
d) Cas particuliers : Dans certains cas, la procédure de découpage est plus longue.
Dans certains cas, la procédure de découpage est plus longue. En effet, si par exemple A est au-dessus à gauche de la pyramide, B dans la pyramide de vision, il sera nécessaire de calculer l'intersection avec le plan supérieur et le plan gauche. Détaillons la marche à suivre :
En effet, si par exemple A est au-dessus à gauche de la pyramide, B dans la pyramide de vision, il sera nécessaire de calculer l'intersection avec le plan supérieur et le plan gauche. Détaillons la marche à suivre :






